全变分（Total variation）在图像去噪算法中的应用

在图像复原过程中，图像上的一点点噪声可能就会对复原的结果产生非常大的影响，因为很多复原算法都会放大噪声。Rudin等人于1992年提出全变分（TV）方法，该方法基于这样一个事实：一个含有噪声的信号相对于其未受噪声影响的信号，它的全变分值要更大,。信号的全变分值被定义为：

TV (u) = \iint | ▽ u | d x d y = \iint \sqrt{u_{x}^{2} + u_{y}^{2}} d x d y

即其梯度绝对值的总和较大。因此如果能找到一个与原始信号相似且全变分较小的信号，即可作为原始信号的降噪结果。全变分去噪(Total Variation Denoising)于1992年由L.I. Rudin、S. Osher和E. Fatemi提出，因此亦称为ROF模型。该算法的优势是可以在去除噪声的同时保留边缘信息，即使在低信噪比（噪声超过真实信号）的情况下，依然能有效地去噪和保留边缘。

全变分的数值可以代表一个图像的平滑程度，举例来说，一张每个像素点值都相同的图像，即这张图没有任何起伏，那其全变分值就为0。TV值越小，平滑度越高。

对于一张含有噪声的图像，若已知信号具有一定的平滑性（对于很多真实图像是满足的），就可以利用全变分方法进行去噪。使用拉格朗日乘子法：

min J (u) = \iint \sqrt{u_{x}^{2} + u_{y}^{2}} d x d y + \frac{λ}{2} \iint (u - u_{0})^{2} d x d y

求解这个其欧拉-拉格朗日方程，可以得到：
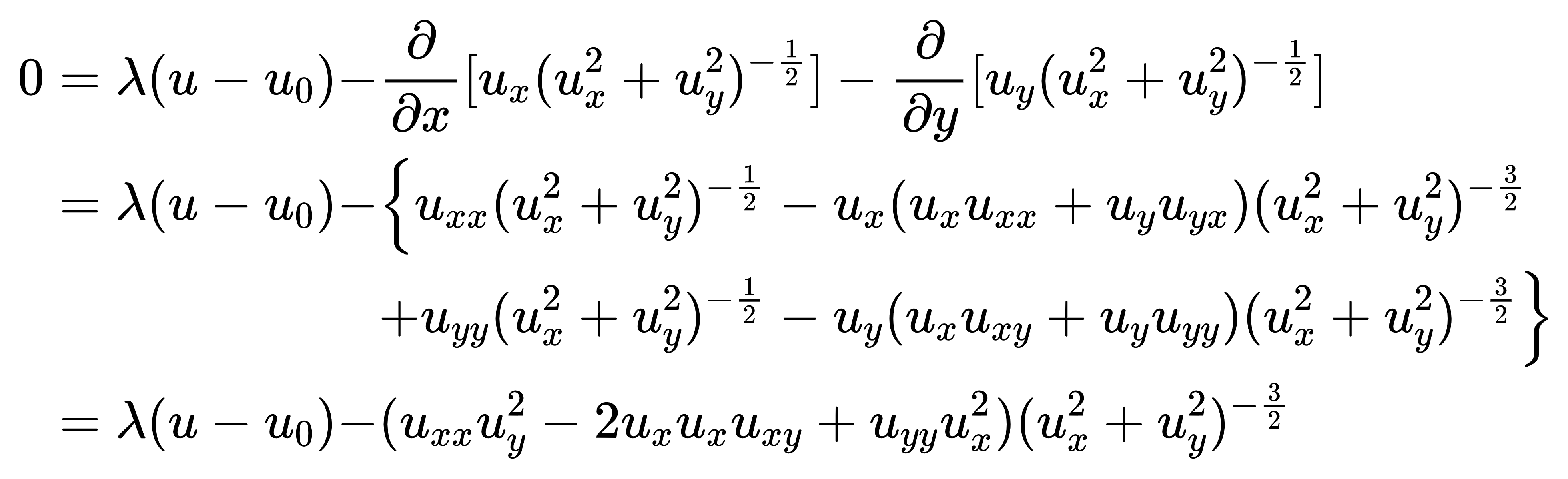
求解这个其欧拉-拉格朗日方程.png

也可以写成更简便的形式：

- \nabla \frac{\nabla u}{| \nabla u |} + λ (u - u_{0}) = 0

利用梯度下降法进行迭代，有限差分求近似解：

u_{(} i, j)^{(n + 1)} = u_{(} i, j)^{n} - Δ t λ^{n} (u_{(} i, j)^{n} - u_{0} (i, j)) + Δ t (▽ \cdot ((▽ u_{(} i, j)^{n}) / (| ▽ u_{(} i, j)^{n} |)))

使用matlab验证该方法，先对原始图像添加高斯噪声，之后使用全变分方法去噪，并计算PSNR（峰值信噪比）和SSIM（结构相似度）来说明去噪的效果。

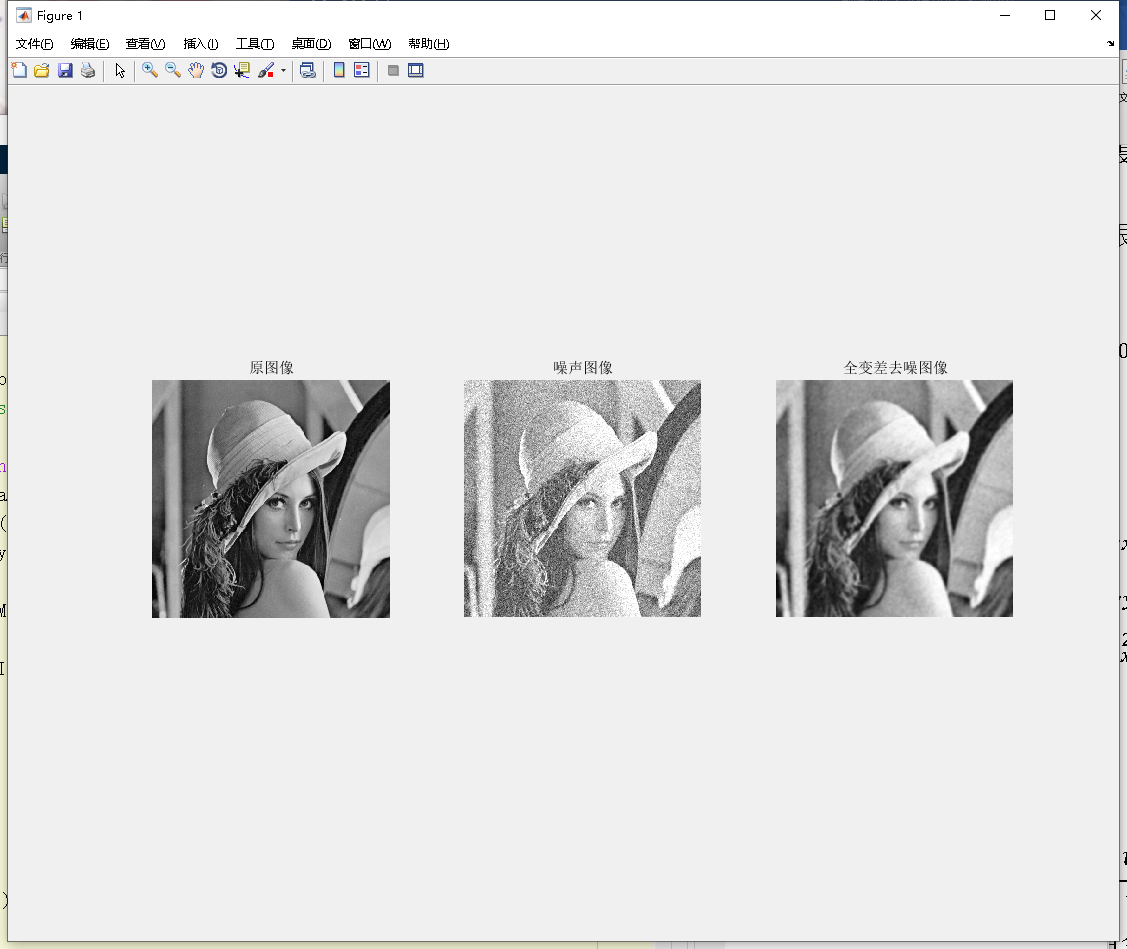
原图，噪声图像，全变分去噪结果展示.png
图1.原图，噪声图像，全变分去噪结果展示

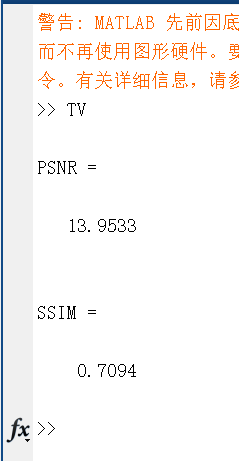
TV去噪的图像和原图像计算PSNR和SSIM.png
图2.TV去噪的图像和原图像计算PSNR和SSIM

可以看出，TV去噪效果是比较好的，在保留细节同时有效祛除了噪声。缺点是会使得复原的图像过于光滑，对于细节较多的图像来说会使复原后的图像丢失细节。

全变分的另一种应用是作为正则项，作为正则项时常在图像复原，图像去噪中应用，作用就是保持图像的光滑性，消除图像复原可能带来的伪影。缺陷在于会使得复原的图像过于光滑，在一些细节比较多的图像中会使得复原后的图像丢失细节。

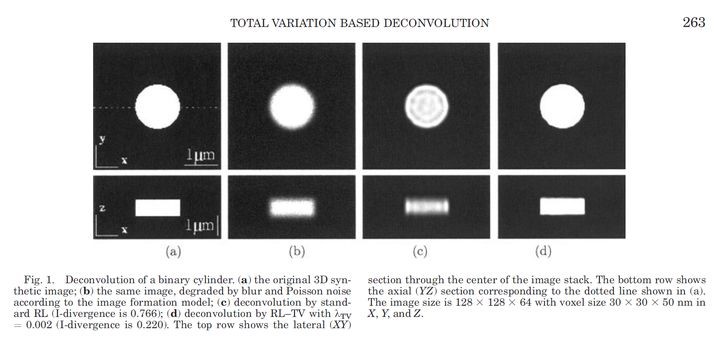
加了TV正则项以后的图像复原结果和不加的差异.jpg
图3 加了TV正则项以后的图像复原结果和不加的差异，图(a)是原始图像，图(b)在原图像上加了一定程度的模糊和噪声，图(c)是不加TV项的复原结果，可以看到有一圈一圈的伪影，这是我们不想要的。图(d)是加了TV项以后的复原结果，没有伪影，复原结果基本和原图像相同。

参考文献
[1] Dey N, Blancferaud L, Zimmer C, et al. Richardson-Lucy Algorithm With sTotal Variation Regularization for 3D Confocal Microscope Deconvolution[J]. Microscopy Research and Technique, 2006, 69(4): 260-266.
[2] Rudin, Leonid I., Stanley Osher, and Emad Fatemi. "Nonlinear total variation based noise removal algorithms." Physica D: nonlinear phenomena 60.1-4 (1992): 259-268.
[3] 总变差去噪 - 维基百科，自由的百科全书 (wikipedia.org)
[4]全变分（TV）模型原理与C++实现_cyh706510441的专栏-CSDN博客_全变分正则化
[5]TV和BTV（全变分和双边全变分） - ostartech - 博客园 (cnblogs.com)
[6]如何理解全变分（Total Variation，TV）模型？ - 知乎 (zhihu.com)
[7]从欧拉-拉格朗日方程到理论力学和全变分约束降噪 - 知乎 (zhihu.com)
[8]Total Variation_weixin_42447651的博客-CSDN博客